為了講解真正有用的晶格密碼學,我們需要先了解「多項式環」與「多項式商環」。不過不用緊張,他跟我們之前看到的整數商環非常類似!我們今天先著重討論多項式環。明天來討論多項式商環
回顧以前的整數商環,
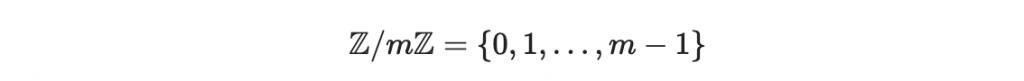
我們知道裡面的環加法就是模加法,環乘法就是模乘法:

在那時,我們說到所謂的「環」由三個部件組合而成,分別是:「集合」、「環加法」、以及「環乘法」,並滿足一些跟整數很像的條件。因此,我們在學習新的環時,我們只需注意這三個部件即可。
數學上我們常用以下符號來代表全部整係數多項式的集合:
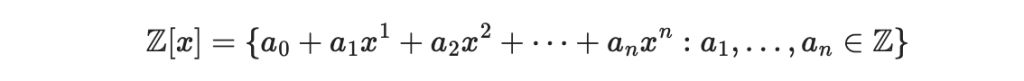
(註:以上集合內的多項式都是有限次方)
而我們中學時期就已經學過多項式加法與多項式乘法,所以很自然地這裡就形成一個環:
集合是剛剛的整係數多項式集合、
環加法是多項式加法、
環乘法是多項式乘法。
接著,我們可以擴展討論的範圍:例如有理係數多項式集合:
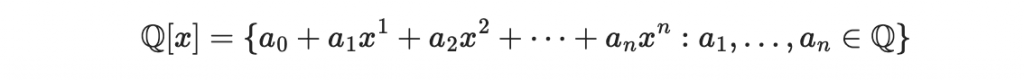
實係數多項式集合:
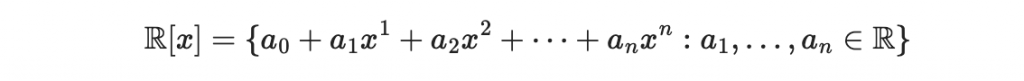
複係數多項式集合:
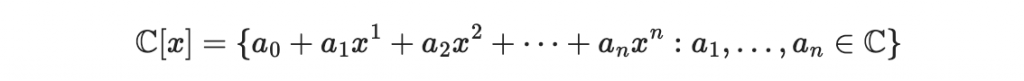
以上這些多項式集合,結合我們中學學過的加法與乘法,自然構成有理係數多項式環、實係數多項式環、複係數多項式環。
是不是很簡單?😀
甚至更廣泛地考慮「某個環」 R ,然後把這個環裡面的元素當作係數,形成以下 R 係數多項式集合:
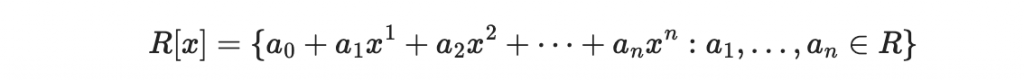
多項式加法還是可以用,因為 R 有他自己的環加法;多項式乘法還是可以用,因為 R 有他自己的環乘法與環加法。你看,這就做出一個 R 係數多項式環。
在這系列文章裡,最重要的莫過於以下的多項式環:
考慮某個模除 q 的整數環:
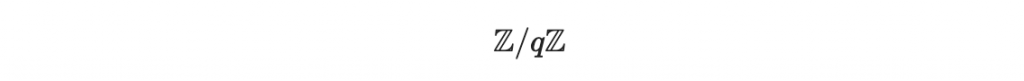
把這裡面的數字當作係數,形成:
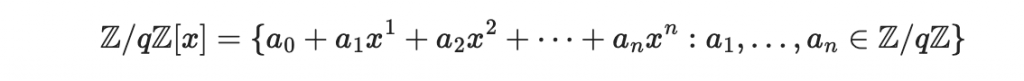
你就得到一個(我覺得中文很難翻譯)「係數模除 q 的多項式環」!
這個環實在是很重要喔,所以我們要舉幾個計算的例子:
考慮以下兩個在係數模除 3 的多項式環內的多項式:
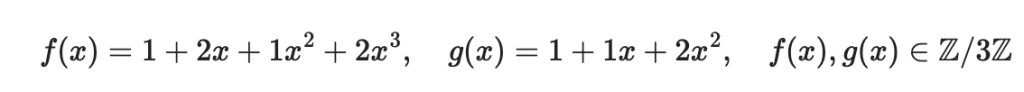
這兩個多項式的環加法結果為:
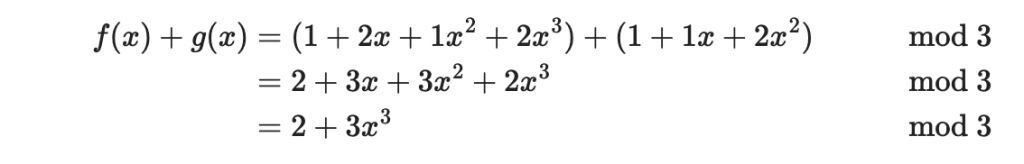
第二個等號是根據正常的多項式加法,第三個等號是對係數進行模除。
這兩個多項式的環乘法結果為:
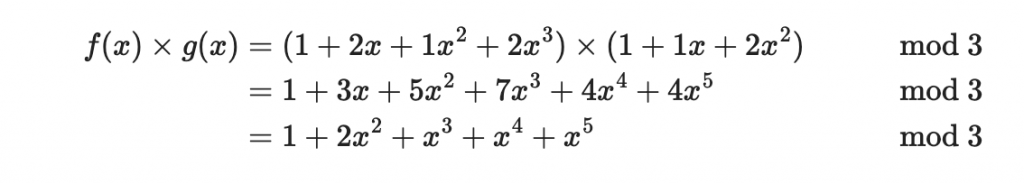
第二的等號是根據正常的多項式乘法,第三個等號是對係數進行模除。
接著,我們來看看如何使用 SageMath 來定義剛剛這個多項式環,並進行對應的計算:
首先,我們先建構多項式環的類別:
# 定義多項式環,係數模 197
q = 197
R_q = quotient(ZZ, q*ZZ)
R_q_poly = PolynomialRing(R_q, x); # 分別代表係數環與未知數的符號
print(R_poly)
# Outputs:
# Univariate Polynomial Ring in x over Ring of integers modulo 197
輸出的結果翻譯為:
Univariate Polynomial Ring : 單變數多項式環
in x : 以 x 為變數
over Ring of integers modulo 197 : 係數是模除 197 的整數環
接著我們來構造其中的元素
# 定義多項式 f(x) 和 g(x)
f = 105*x^3 + 110*x^2 + 115*x + 120
g = 120*x^3 + 130*x^2 + 140*x + 150
print(type(f))
print(f)
print(list(f))
# Outputs:
# <class 'sage.rings.polynomial.polynomial_zmod_flint.Polynomial_zmod_flint'>
# 105*x^3 + 110*x^2 + 115*x + 120
# [120, 115, 110, 105]
你可以在第二個以及第三個輸出裡看到,我們可以用多項式的寫法來輸出,也可以用列表來輸出。其中多項式的寫法預設是降冪排列,列表的寫法是升冪。我個人更習慣使用升冪的列表輸出。
值得一提的是:SageMath 並不會搞混這兩種輸出法:
print(R_q_poly([120, 115, 110, 105]) == f)
# Outputs: True
最後,我們來進行環加法與環乘法的計算:
# 多項式加法
add_result = f + g
# 多項式乘法
mul_result = f * g
# 顯示加法和乘法結果
print(add_result)
print(mul_result)
# Outputs:
# 28*x^3 + 43*x^2 + 58*x + 73
# 189*x^6 + 58*x^5 + 51*x^4 + 21*x^3 + 132*x^2 + 166*x + 73
今天主要內容先到這裡,因為接下來要講的是「多項式商環」,今天再寫下去篇幅就不夠了。而多項式商環講解完畢後,我們就可以進到「吾乃數論學家密碼系統」,是真正可用的晶格密碼系統之一!

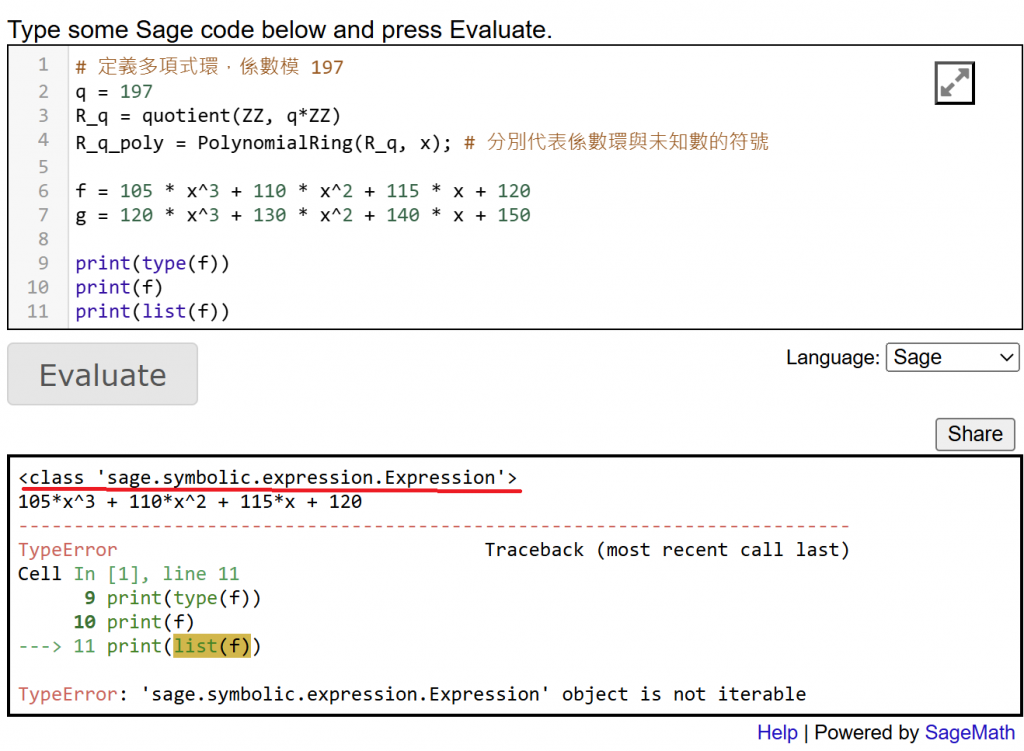
請問為什麼 type(f) 的結果會和你的執行結果不同呢?
我搞懂了要改成這樣
f = R_q_poly(105 * x^3 + 110 * x^2 + 115 * x + 120)
g = R_q_poly(120 * x^3 + 130 * x^2 + 140 * x + 150)
不知是否為版本問題,在我使用 x 為未知數來寫出 f 時,系統就會知道 f(x) 是屬於我剛剛定義的那個環。好!總之,能 work 就好!